Section 8 Distribution of the Sample Mean

Distribution of Sample Mean

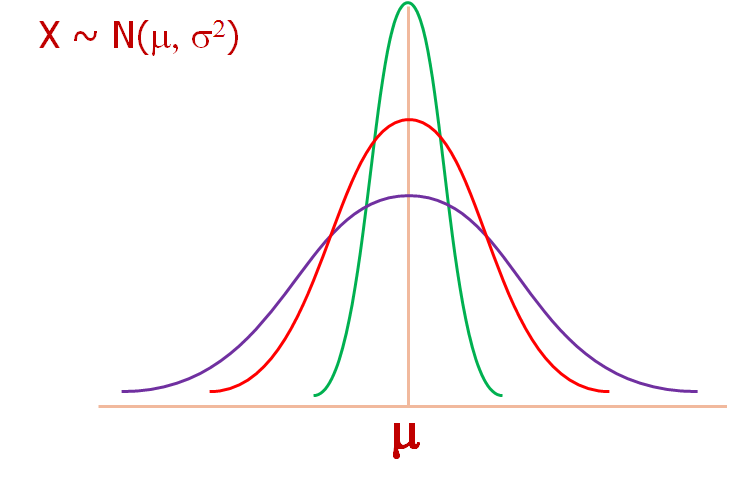
\[\Huge If \hspace{6mm} X \sim Normal(\mu, \sigma^2)\]

\[\Huge Then \hspace{6mm} \bar{x} \sim Normal(\mu, \frac{\sigma^2}{n})\]

• For bigger samples, the standard error is less, and therefore your estimate is likely to be closer to the true mean.

• Large samples give better information than small samples.

• Note also, the larger the variability in the data the, larger the sample required to estimate the mean with given precision.