Section 17 Hypothesis Testing: Decision & Power
17.2 Statistical Power

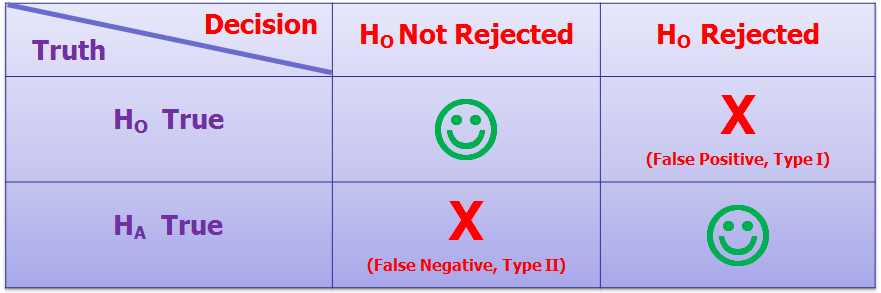
The Statistical Power of any test is defined as the probability of making the correct decision (e.g. detecting a difference) when the assumption being tested (e.g. no difference) is false.
The power of a statistical test is the probability of rejecting the null hypothesis \(\large H_0\) when the alternative hypothesis \(\large H_A\) is true.
If we repeat an experiment many times, the Statistical Power is the expected proportion of experiments for which: - the P-value < 0.05 - The 95% confidence interval for the parameter is sufficiently narrow
Statistical Power depends on - the variability in the measured outcome(s) - the design of the study - what you want to find out from the study - acceptable type 1 and 2 error