Section 44 Model Selection: Backward Stepwise Selection



44.1 Statistical Model

\[ \large y_{i} = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi} + \epsilon_{i} \]

\[ i = 1,...,n; \space p = \space number \space of \space predictors \]


44.2 Steps

  1. Fit a Full model \(M_p\) which contains all \(p\) predictors.

  2. For \(k = p,p-1,...,1\)

    1. Consider all \(k\) models that contain all but one of the predictors in \(M_k\), for a total of \(k-1\) predictors.

    2. Choose the best model \(M_{k-1}\) among these \(k\) models based on the smallest RSS, or equivalently, largest \(R^2\).

  3. Select a single best model from among \(M_0, M_1, ..., M_p\) models using the criteria Adjusted \(R^2\), Mallow’s Cp, AIC or BIC.

44.3 Comments

  • Like forward stepwise selection, this approach fits \(1 + p(p+1)/2\) models.

  • The backward stepwise selection also provides an efficient alternative to best subset selection.

  • All models within backward selection approach are nested.

  • However, it It is not guaranteed to find the best possible model out of all \(2^p\) models containing subsets of the \(p\) predictors.

  • Backward selection requires that the number of samples \(n\) is larger than the number of variables \(p\) (\(n >> p\)).


44.4 R implementation


library(leaps)

BP <- read.csv('data/BP.csv')
# Remove NA values from all variables
BP <- na.omit(BP)
BP$DM <- as.factor(BP$DM)

# Subset the data
BP <- BP[,-1]

# Backward stepwise selection
bwd.fm <- regsubsets(SBP ~ ., data=BP, 
                      nbest=1, nvmax=6, intercept=TRUE,
                      method='backward')
bwd.summary <- summary(bwd.fm)

bwd.summary
Subset selection object
Call: regsubsets.formula(SBP ~ ., data = BP, nbest = 1, nvmax = 6, 
    intercept = TRUE, method = "backward")
6 Variables  (and intercept)
                Forced in Forced out
EthnicAsian         FALSE      FALSE
EthnicCaucasian     FALSE      FALSE
Age                 FALSE      FALSE
Income              FALSE      FALSE
BMI                 FALSE      FALSE
DM2                 FALSE      FALSE
1 subsets of each size up to 6
Selection Algorithm: backward
         EthnicAsian EthnicCaucasian Age Income BMI DM2
1  ( 1 ) " "         " "             " " " "    "*" " "
2  ( 1 ) " "         " "             " " " "    "*" "*"
3  ( 1 ) " "         " "             "*" " "    "*" "*"
4  ( 1 ) " "         " "             "*" "*"    "*" "*"
5  ( 1 ) " "         "*"             "*" "*"    "*" "*"
6  ( 1 ) "*"         "*"             "*" "*"    "*" "*"
coef(bwd.fm, id=6)
    (Intercept)     EthnicAsian EthnicCaucasian             Age          Income             BMI             DM2 
   -3.858060268    -0.002753277    -0.013373729     0.903319577    -0.003045831     2.348833049     4.073927322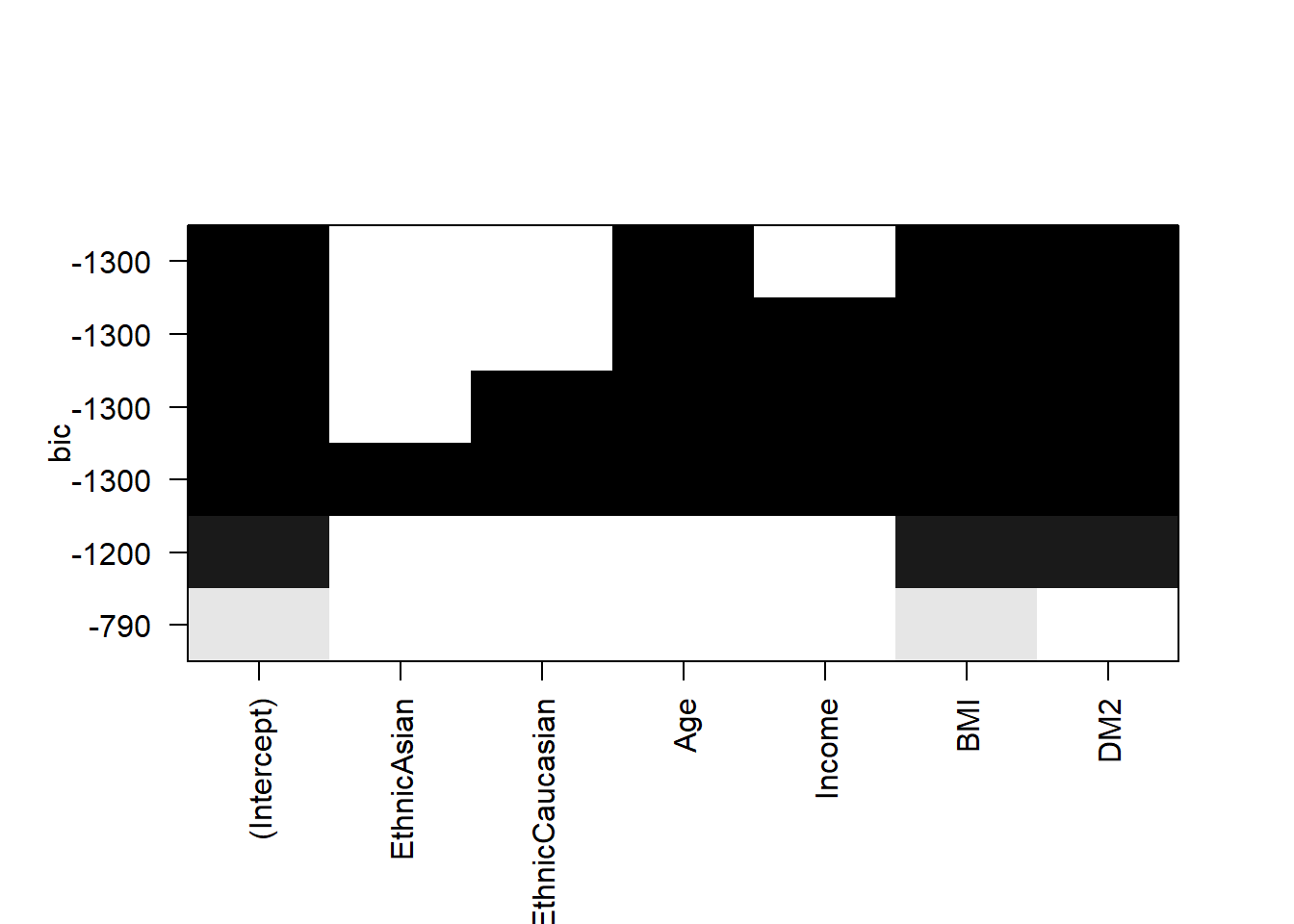 
# Plot of Backward stepwise selection
plot(bwd.fm, scale='bic')

# Customised plot
par(mfrow=c(2,2))
xlab <- 'Number of X-variables'

plot(x = bwd.summary$rss, 
     xlab=xlab, ylab='RSS', 
     type='l', col='blue')
index <- which.min(bwd.summary$rss)
points(x = index, y = bwd.summary$rss[index], 
       col='red', cex=2, pch=20)

plot(x=bwd.summary$adjr2, 
     xlab=xlab, ylab='Adjusted R2', 
     type='l', col='blue')
index <- which.max(bwd.summary$adjr2)
points(x = index, y = bwd.summary$adjr2[index], 
       col='red', cex=2, pch=20)

plot(x=bwd.summary$cp, 
     xlab=xlab, ylab='Mallow Cp', 
     type='l', col='blue')
index <- which.min(bwd.summary$cp)
points(x = index, y = bwd.summary$cp[index], 
       col='red', cex=2, pch=20)

plot(x=bwd.summary$bic, 
     xlab=xlab, ylab='BIC', 
     type='l', col='blue')
index <- which.min(bwd.summary$bic)
points(x = index, y = bwd.summary$bic[index], 
       col='red', cex=2, pch=20)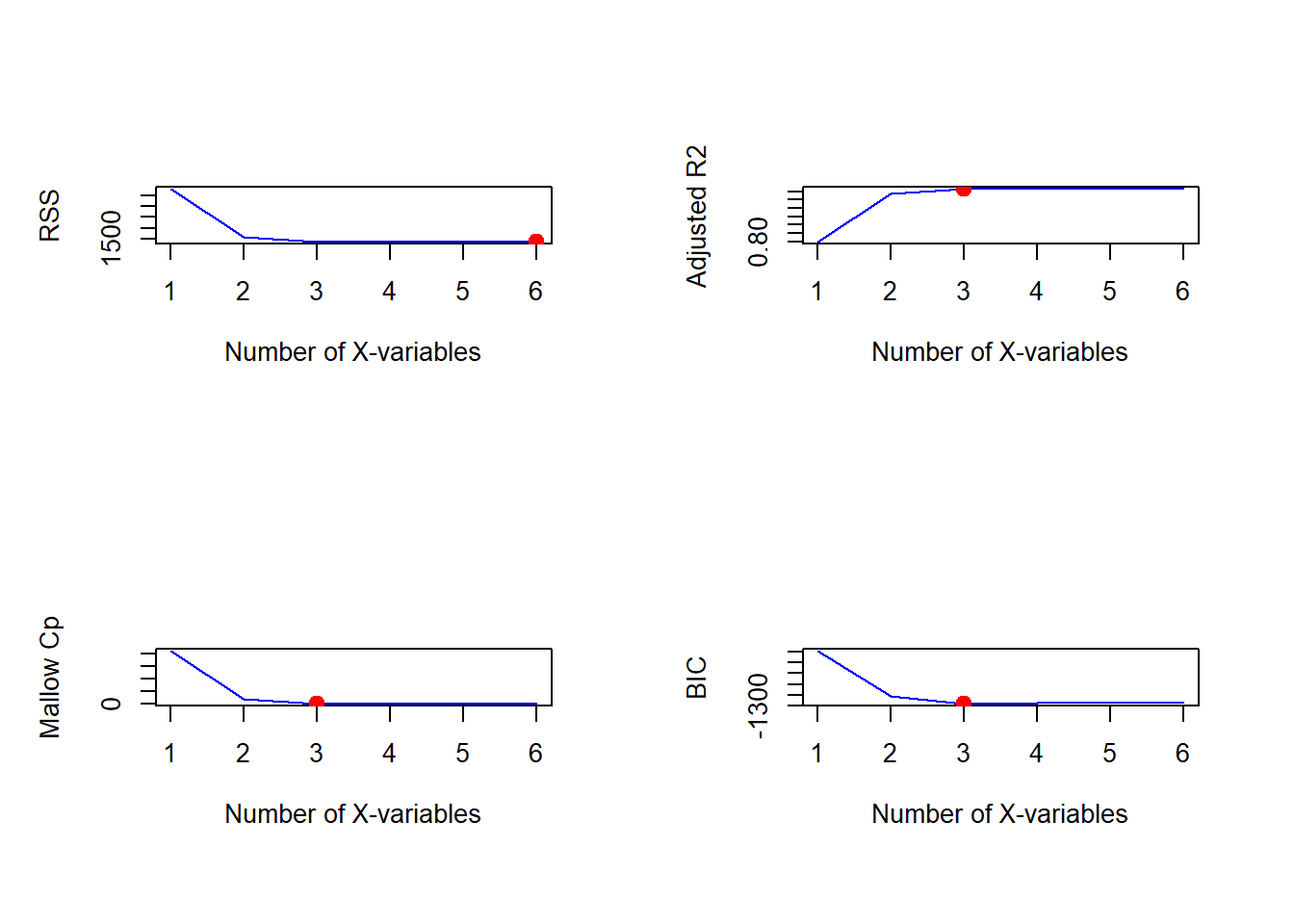

coef(bwd.fm, id=3)
(Intercept)         Age         BMI         DM2 
 -3.9018887   0.9022749   2.3487465   4.0731999