Section 19 Hypothesis Testing - Two Samples: Steps

19.1 Model

SBP = Overall Mean + Sampling Variability

$$\large y_{j} = \mu + \epsilon_{j}$$

SBP = Overall mean + Group effect + Sampling variability

$$\large y_{ij} = \mu + \beta_{i} + \epsilon_{ij}$$

$\large y_{ij}$ = j -th observation (replicate) in the i -th treatment

$\large \mu$ = overall mean effect

$\large \beta_{i}$ = effect of treatment group i

$\large \epsilon_{ij} \sim NID(0, \sigma^2)$

$\large i$ = treatment index; i: 1, 2

$\large j$ = observation index within each treatment; j: 1 to n

19.2 Assumptions

• Values within each group are independent and normally distributed

• Variances of the two groups are equal

19.3 Steps of Hypothesis testing

1. Identify the parameter of interest

2. Define $\large H_O$ and $\large H_A$

3. Define a significance level $\large \alpha$

4. Calculate an estimate of the parameter

5. Determine an appropriate test statistic, its distribution when $\large H_O$ is correct, calculate the value of test statistic from the sample

6. Obtain the probability under the distribution of the test statistic

7. Compare the observed probability given $\large \alpha$ and conclude

19.4 Two Samples, Unknown Variance

Inference for a difference in means of two Normal distributions when variances are unknown

19.5 Steps of Hypothesis testing: Details

1. Identify the parameter of interest: Population mean $\large \mu$

2. Define $\large H_O$ and $\large H_A$

$$\large H_O: \mu_1 = \mu_2$$

$$\large H_A: \mu_1 \ne \mu_2$$

3. Define $\large \alpha$

$$\large \alpha = 0.05$$

4. Calculate an estimate of the parameter

Sample Mean: $$\large \bar{x_1} = \frac{1}{n}\sum\limits_{i=1}^{n} x_{1i}$$ $$\large \bar{x_2} = \frac{1}{n}\sum\limits_{i=1}^{n} x_{2i}$$

Pooled Sample Standard Deviation:

Scenario 1: Variances of TWO samples are equal

$$\large s = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}}$$

Scenario 2: Variances of TWO samples are NOT equal

$$\large s = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}$$

Where: $\large s_1^2$ and $\large s_2^2$ are variances from Sample 1 and Sample 2, respectively.

5. Determine test statistic, its distribution when $\large H_O$ is correct, calculate the value of test statistic from the sample.

$$\large t_{Cal} = \frac{(\bar{x_1}-\bar{x_2}) - (\mu_1 - \mu_2)} {s\sqrt{1/n_1+1/n_2}}$$

$$\large t_{Cal} = \frac{(\bar{x_1}-\bar{x_2})} {s\sqrt{1/n_1+1/n_2}}$$

• Note - The test statistic is the difference of Observed Difference & Expected Difference - The test statistic represents the ratio of signal to error - The test statistic is centred and scaled

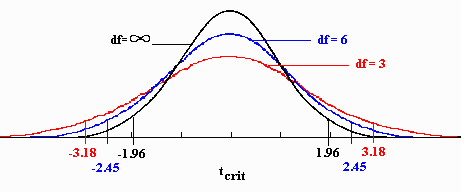
Distribution of the test statistic

Scenario 1: Variances of TWO samples are equal

$$\large t \hspace{2mm} distribution \hspace{2mm} with \hspace{2mm} (n_1+n_2-2) \hspace{2mm} df$$

Scenario 2: Variances of TWO samples are NOT equal

The degrees of freedom will be computed.

$$\large degrees \hspace{2mm} of \hspace{2mm} freedom = \frac{(s_1^2 + s_2^2)} {s_1^2/(n_1-1) + s_2^2/(n_2-1)}$$

$$\large t \hspace{2mm} distribution \hspace{2mm} with \hspace{2mm} computed \hspace{2mm} df$$

6. Obtain the probability under the distribution of the test statistic (two-tailed probability)

$$\large 2*pt(q = |t_{Cal}|, \space df, \space lower.tail=FALSE)$$

7. Compare the observed probability given the $\large \alpha$ and conclude

Find the probability that $\large t$ is less than or equal to $\large |t_{Cal}|$ from $\large t$ distribution with $\large (n_1+n_2-2)$ degrees of freedom for the Scenario 1. Use integer values of degrees of freedom for the Scenario 2.