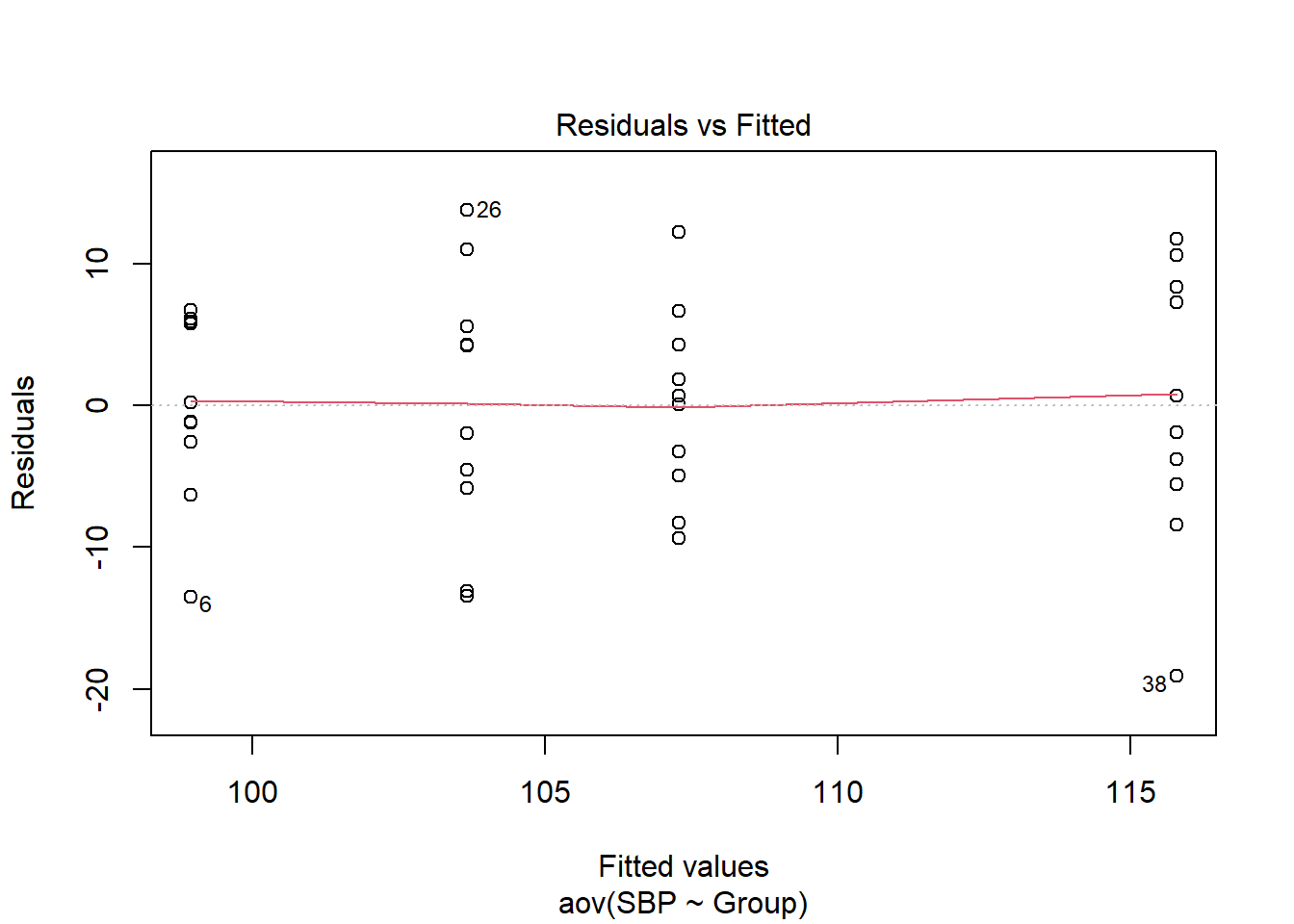
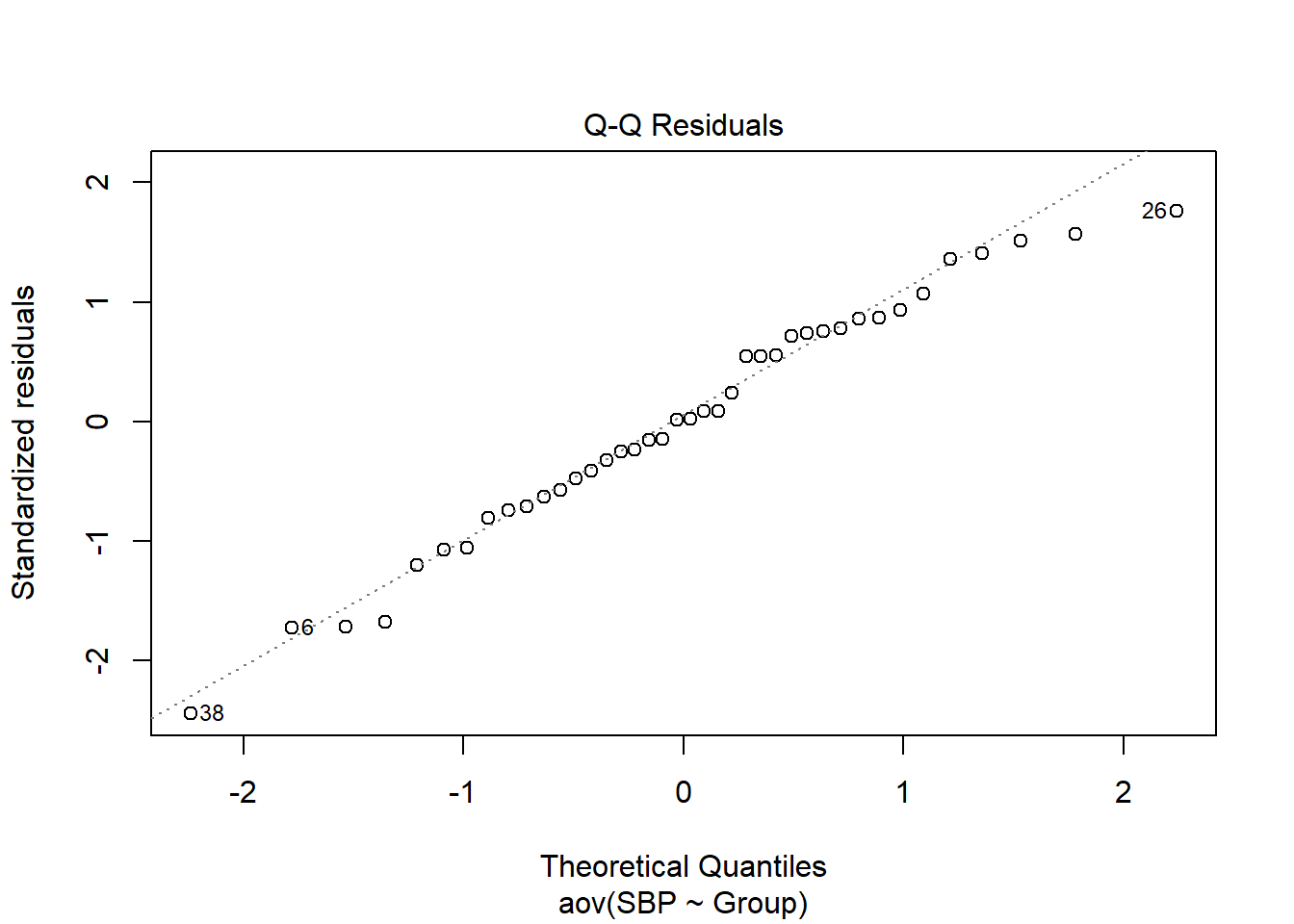
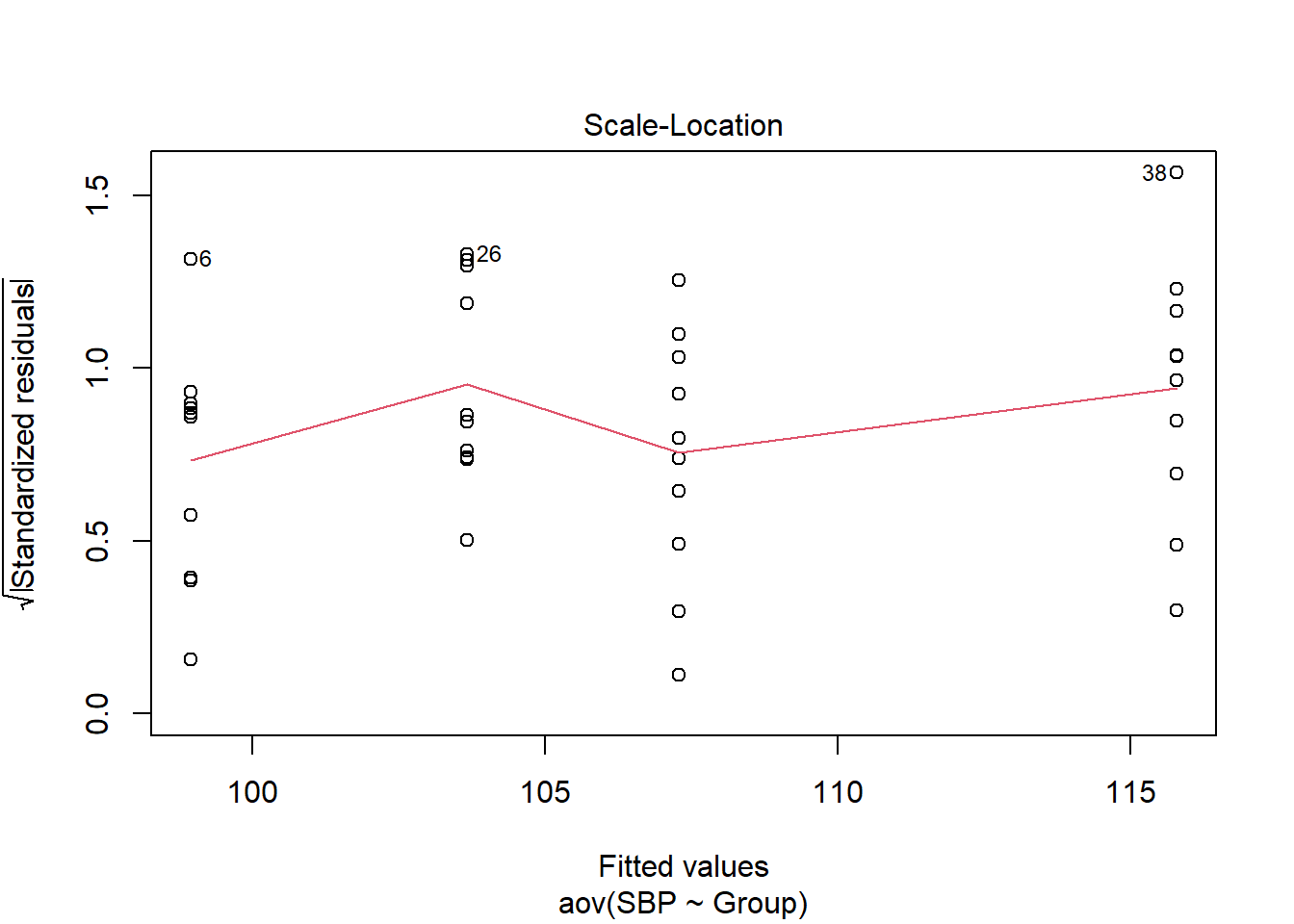
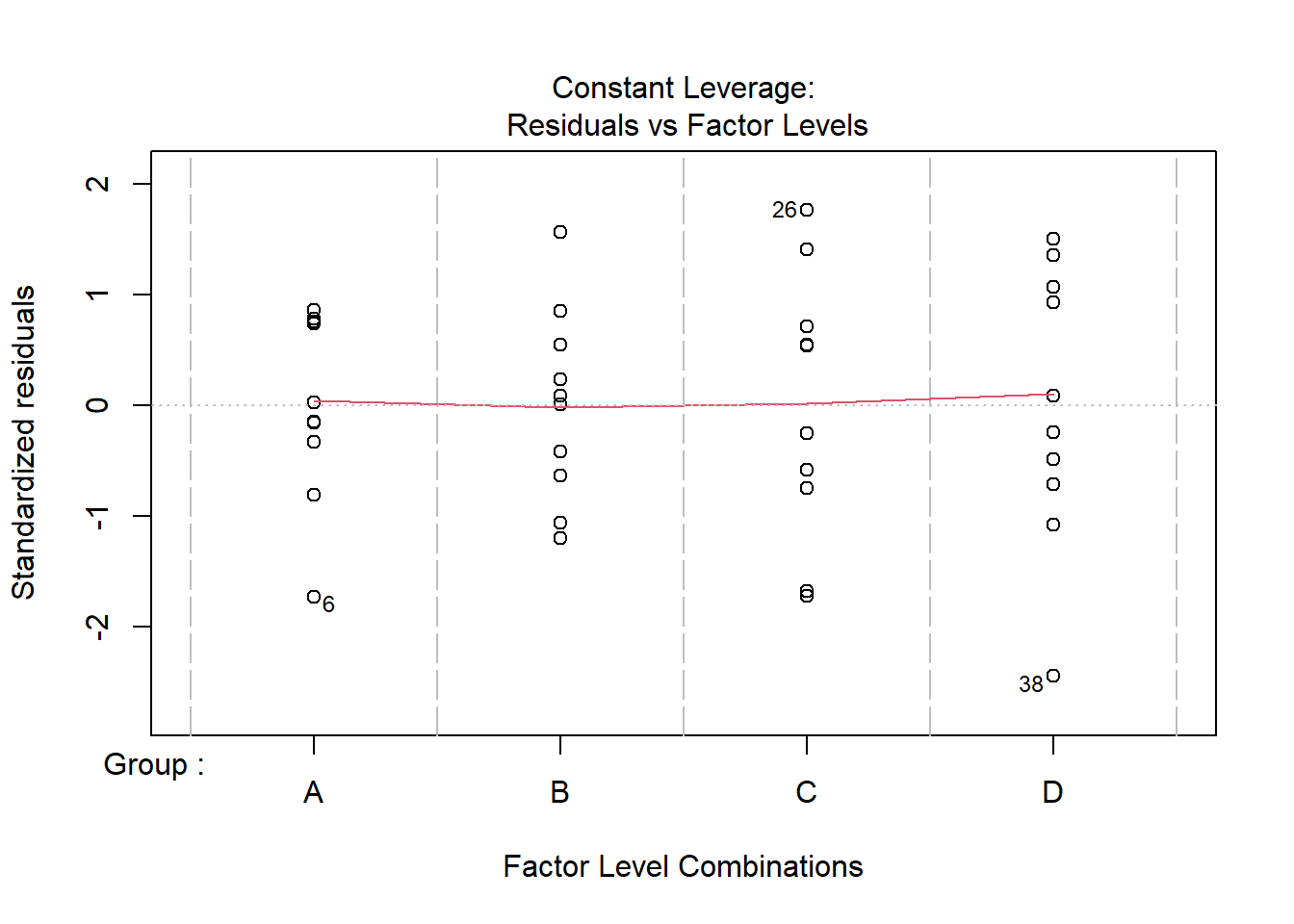
Section 38 One-way ANOVA: function aov

• The function aov also fits an analysis of variance model by a call to lm for each stratum for a balanced experimental design.

• This provides a wrapper to lm for fitting linear models to balanced or unbalanced experimental designs.

• The main difference from lm is in the way print, summary and other R objects are handled and presented: this is expressed in the traditional language of the analysis of variance rather than that of linear models.

• If the formula contains an Error term, this is used to specify error strata, and appropriate models are fitted within each error stratum.

• If you have multiple error terms in the data, then the aov is the appropriate function to fit anova model.

38.1 Estimates: Effects

\[ \large fm.aov \leftarrow aov(SBP \sim Group, \space data=BP) \]

\[ \large aov(fm.aov) \]

38.2 Using aov function

# function `aov`
fm.aov <- aov(SBP ~ Group, data = BP)


# function `aov` with error stratum

# fm1.aov <- aov(SBP ~ Group + Error(factor(ID)), data=BP)


# Analysis of variance
summary(fm.aov)

            Df Sum Sq Mean Sq F value   Pr(>F)    
Group        3   1522   507.2   7.498 0.000506 ***
Residuals   36   2435    67.6                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Estimates of effects
model.tables(fm.aov, type = "effects", se = TRUE)

Tables of effects

 Group 
Group
     A      B      C      D 
-7.484  0.868 -2.754  9.371 

Standard errors of effects
        Group
        2.601
replic.    10

# Estimates of means
model.tables(fm.aov, type = "means", se = TRUE)

Tables of means
Grand mean
         
106.4223 

 Group 
Group
     A      B      C      D 
 98.94 107.29 103.67 115.79 

Standard errors for differences of means
        Group
        3.678
replic.    10

# Plot of residuals
plot(fm.aov)