Section 26 One-way ANOVA: Steps
26.1 Model
SBP = overall mean + sampling variability
\[ \large y_{j} = \mu + \epsilon_{j} \]
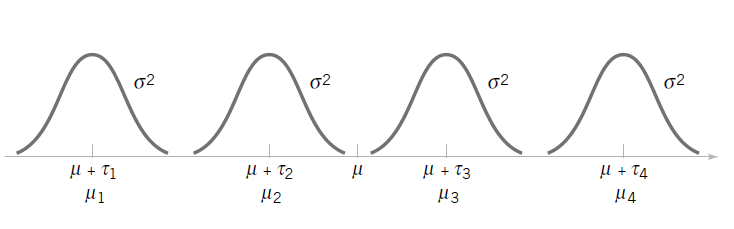
SBP = overall mean + Group effect + sampling variability
\[ \large y_{ij} = \mu + \tau_{i} + \epsilon_{ij} \]
\(\large i\) = treatment index; i: 1 to g
\(\large j\) = observation index within treatment; j: 1 to n
\(\large y_{ij}\) = j -th observation (replicate) in the i -th treatment
\(\large \mu\) = overall mean effect
\(\large \tau_{i}\) = effect of treatment group i
\(\large \epsilon_{ij} \sim NID(0, \sigma^2)\)