Section 42 Post hoc analysis: R implementation

42.1 Familywise Error Rate

fm.aov <- aov(SBP ~ Group, data = BP)

# Analysis of variance
anova(fm.aov)

Analysis of Variance Table

Response: SBP
          Df Sum Sq Mean Sq F value    Pr(>F)    
Group      3 1521.6  507.21  7.4983 0.0005059 ***
Residuals 36 2435.2   67.64                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# No correction

pairwise.t.test(x = BP$SBP, g = BP$Group, p.adjust.method = "none")

    Pairwise comparisons using t tests with pooled SD 

data:  BP$SBP and BP$Group 

  A       B      C     
B 0.0292  -      -     
C 0.2067  0.3313 -     
D 5.3e-05 0.0266 0.0022

P value adjustment method: none 

# Multiple comparison: Bonferroni correction

pairwise.t.test(x = BP$SBP, g = BP$Group, p.adjust.method = "bonferroni")

    Pairwise comparisons using t tests with pooled SD 

data:  BP$SBP and BP$Group 

  A       B       C      
B 0.17548 -       -      
C 1.00000 1.00000 -      
D 0.00032 0.15975 0.01325

P value adjustment method: bonferroni 

# Multiple comparison: Holm

pairwise.t.test(x = BP$SBP, g = BP$Group, p.adjust.method = "holm")

    Pairwise comparisons using t tests with pooled SD 

data:  BP$SBP and BP$Group 

  A       B       C      
B 0.10650 -       -      
C 0.41333 0.41333 -      
D 0.00032 0.10650 0.01104

P value adjustment method: holm 

# Tukey's HSD Note: Only applicable on the aov object

TukeyHSD(fm.aov)

  Tukey multiple comparisons of means
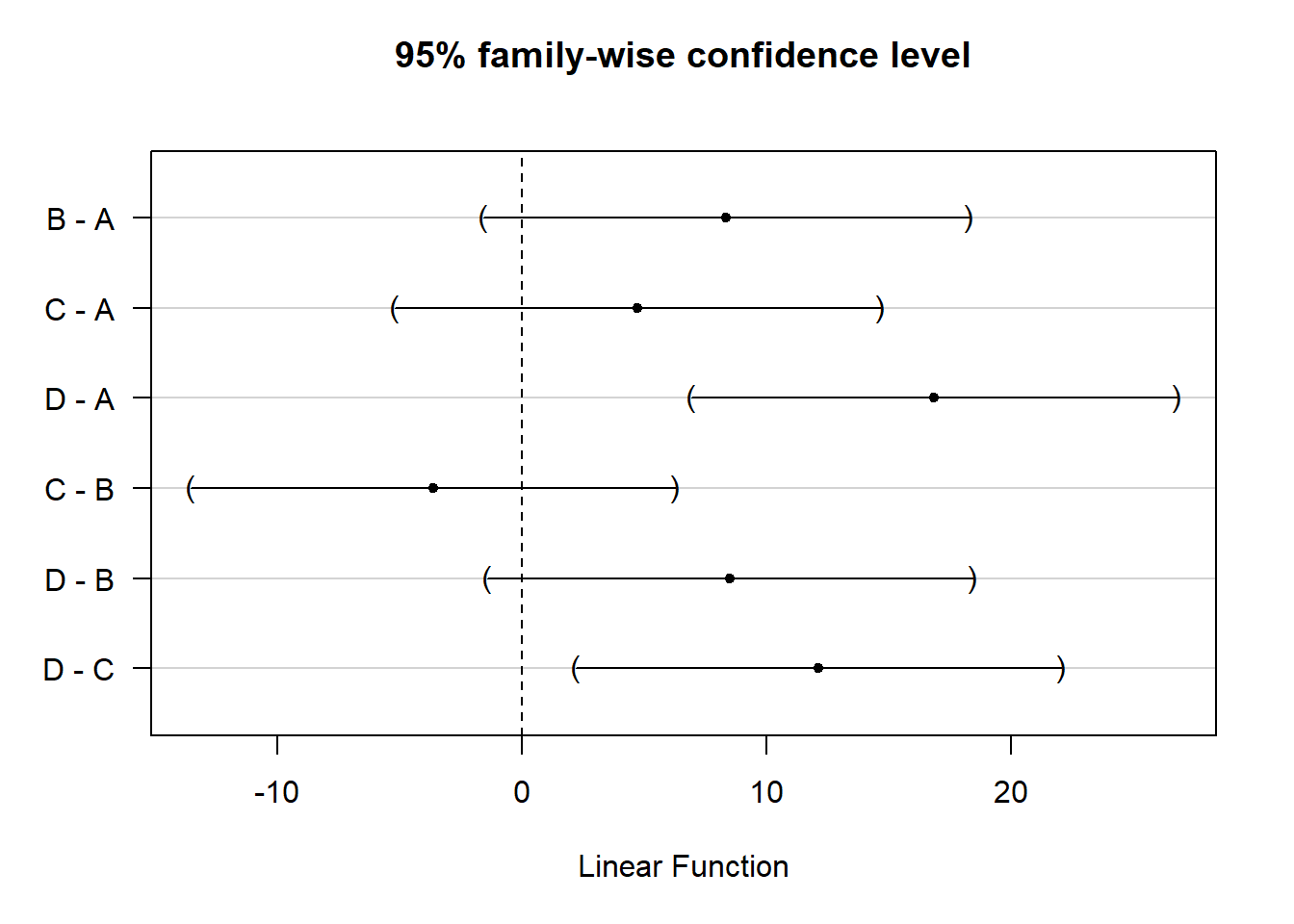
    95% family-wise confidence level

Fit: aov(formula = SBP ~ Group, data = BP)

$Group
      diff        lwr       upr     p adj
B-A  8.352  -1.554098 18.258098 0.1240483
C-A  4.730  -5.176098 14.636098 0.5775956
D-A 16.855   6.948902 26.761098 0.0003004
C-B -3.622 -13.528098  6.284098 0.7589637
D-B  8.503  -1.403098 18.409098 0.1142036
D-C 12.125   2.218902 22.031098 0.0113324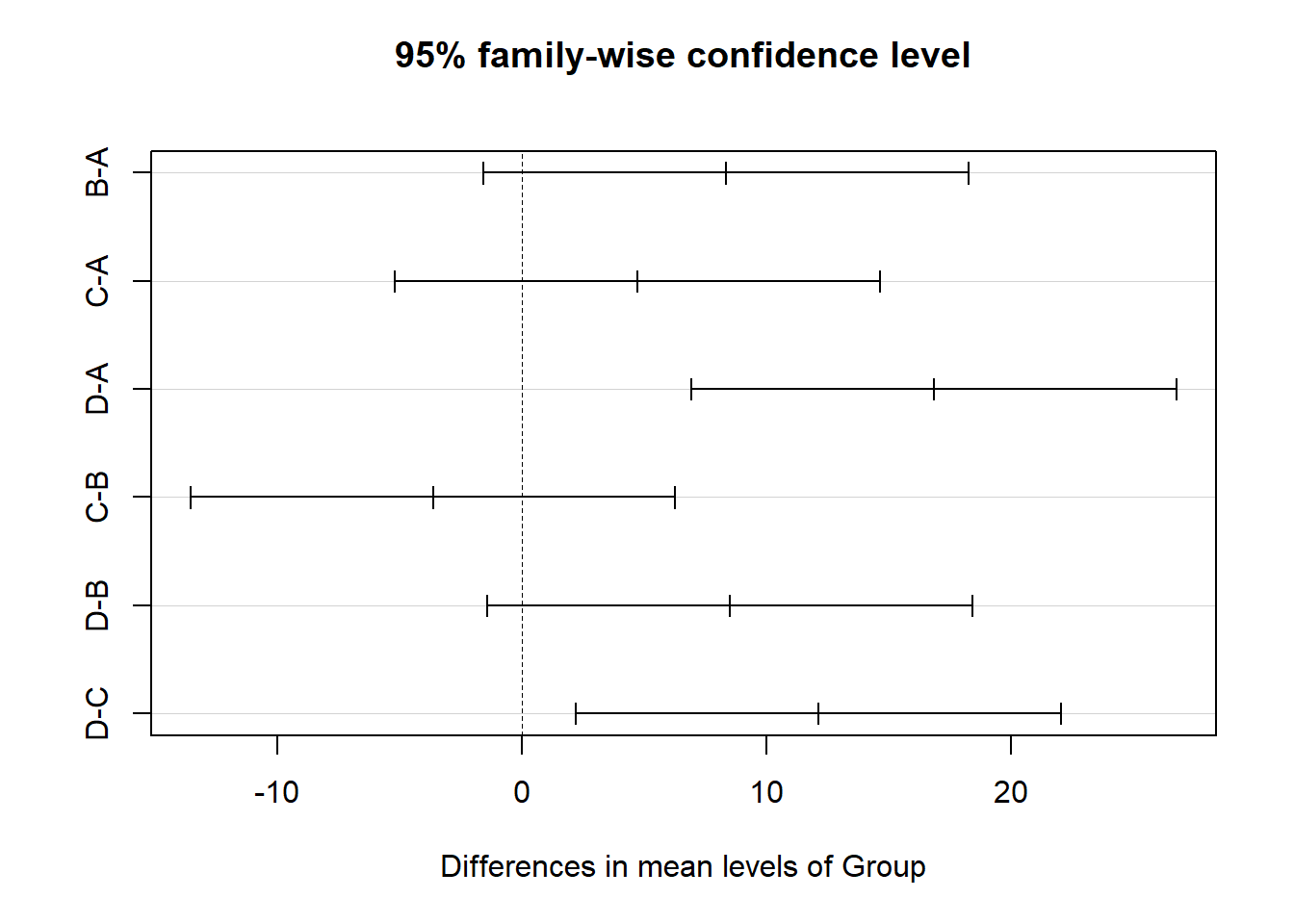

plot(TukeyHSD(fm.aov))

42.2 False Discovery Rate

# Benjamini & Hochberg (1995) BH or fdr

pairwise.t.test(x = BP$SBP, g = BP$Group, p.adjust.method = "BH")

    Pairwise comparisons using t tests with pooled SD 

data:  BP$SBP and BP$Group 

  A       B       C      
B 0.04387 -       -      
C 0.24800 0.33133 -      
D 0.00032 0.04387 0.00662

P value adjustment method: BH 

## Benjamini & Yekutieli (2001)

pairwise.t.test(x = BP$SBP, g = BP$Group, p.adjust.method = "BY")

    Pairwise comparisons using t tests with pooled SD 

data:  BP$SBP and BP$Group 

  A       B       C      
B 0.10748 -       -      
C 0.60759 0.81175 -      
D 0.00079 0.10748 0.01623

P value adjustment method: BY 

42.3 Using library(lsmeans)

require(lsmeans)

fm <- lm(SBP ~ Group, data = BP)

gr.means <- lsmeans(fm, specs = ~Group)


# Esimated means
gr.means

 Group lsmean  SE df lower.CL upper.CL
 A       98.9 2.6 36     93.7      104
 B      107.3 2.6 36    102.0      113
 C      103.7 2.6 36     98.4      109
 D      115.8 2.6 36    110.5      121

Confidence level used: 0.95 

# Comparison of means: No adjustment
contrast(gr.means, method = "pairwise", adjust = NULL)

 contrast estimate   SE df t.ratio p.value
 A - B       -8.35 3.68 36  -2.271  0.0292
 A - C       -4.73 3.68 36  -1.286  0.2067
 A - D      -16.86 3.68 36  -4.582  0.0001
 B - C        3.62 3.68 36   0.985  0.3313
 B - D       -8.50 3.68 36  -2.312  0.0266
 C - D      -12.12 3.68 36  -3.296  0.0022

# Comparison of means: FWER (bonferroni)
contrast(gr.means, method = "pairwise", adjust = "bonferroni")

 contrast estimate   SE df t.ratio p.value
 A - B       -8.35 3.68 36  -2.271  0.1755
 A - C       -4.73 3.68 36  -1.286  1.0000
 A - D      -16.86 3.68 36  -4.582  0.0003
 B - C        3.62 3.68 36   0.985  1.0000
 B - D       -8.50 3.68 36  -2.312  0.1597
 C - D      -12.12 3.68 36  -3.296  0.0132

P value adjustment: bonferroni method for 6 tests 

# Comparison of means: FWER (tukey)
contrast(gr.means, method = "pairwise", adjust = "tukey")

 contrast estimate   SE df t.ratio p.value
 A - B       -8.35 3.68 36  -2.271  0.1240
 A - C       -4.73 3.68 36  -1.286  0.5776
 A - D      -16.86 3.68 36  -4.582  0.0003
 B - C        3.62 3.68 36   0.985  0.7590
 B - D       -8.50 3.68 36  -2.312  0.1142
 C - D      -12.12 3.68 36  -3.296  0.0113

P value adjustment: tukey method for comparing a family of 4 estimates 

# Comparison of means: FDR (BH)
contrast(gr.means, method = "pairwise", adjust = "fdr")

 contrast estimate   SE df t.ratio p.value
 A - B       -8.35 3.68 36  -2.271  0.0439
 A - C       -4.73 3.68 36  -1.286  0.2480
 A - D      -16.86 3.68 36  -4.582  0.0003
 B - C        3.62 3.68 36   0.985  0.3313
 B - D       -8.50 3.68 36  -2.312  0.0439
 C - D      -12.12 3.68 36  -3.296  0.0066

P value adjustment: fdr method for 6 tests 

42.4 Using library(multcomp)

The package multcomp considers a wide range of methods as well as customised contrasts to conduct multiple testing of hypotheses.

require(multcomp)


# Prepare the contrast using Group='Tukey'
mult.test <- glht(fm, linfct = mcp(Group = "Tukey"))


# FWER: tukey
summary(mult.test)

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = SBP ~ Group, data = BP)

Linear Hypotheses:
           Estimate Std. Error t value Pr(>|t|)    
B - A == 0    8.352      3.678   2.271   0.1239    
C - A == 0    4.730      3.678   1.286   0.5776    
D - A == 0   16.855      3.678   4.582   <0.001 ***
C - B == 0   -3.622      3.678  -0.985   0.7590    
D - B == 0    8.503      3.678   2.312   0.1142    
D - C == 0   12.125      3.678   3.296   0.0112 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

# No adjustment
summary(mult.test, test = adjusted("none"))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = SBP ~ Group, data = BP)

Linear Hypotheses:
           Estimate Std. Error t value Pr(>|t|)    
B - A == 0    8.352      3.678   2.271  0.02925 *  
C - A == 0    4.730      3.678   1.286  0.20666    
D - A == 0   16.855      3.678   4.582 5.34e-05 ***
C - B == 0   -3.622      3.678  -0.985  0.33133    
D - B == 0    8.503      3.678   2.312  0.02662 *  
D - C == 0   12.125      3.678   3.296  0.00221 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- none method)

# FWER: bonferroni
summary(mult.test, test = adjusted("bonferroni"))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = SBP ~ Group, data = BP)

Linear Hypotheses:
           Estimate Std. Error t value Pr(>|t|)    
B - A == 0    8.352      3.678   2.271  0.17548    
C - A == 0    4.730      3.678   1.286  1.00000    
D - A == 0   16.855      3.678   4.582  0.00032 ***
C - B == 0   -3.622      3.678  -0.985  1.00000    
D - B == 0    8.503      3.678   2.312  0.15975    
D - C == 0   12.125      3.678   3.296  0.01325 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- bonferroni method)

# FDR: BH
summary(mult.test, test = adjusted("fdr"))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = SBP ~ Group, data = BP)

Linear Hypotheses:
           Estimate Std. Error t value Pr(>|t|)    
B - A == 0    8.352      3.678   2.271  0.04387 *  
C - A == 0    4.730      3.678   1.286  0.24800    
D - A == 0   16.855      3.678   4.582  0.00032 ***
C - B == 0   -3.622      3.678  -0.985  0.33133    
D - B == 0    8.503      3.678   2.312  0.04387 *  
D - C == 0   12.125      3.678   3.296  0.00662 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- fdr method)

# Plot the mean comparisons
plot(print(confint(mult.test)))

     Simultaneous Confidence Intervals

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = SBP ~ Group, data = BP)

Quantile = 2.6954
95% family-wise confidence level
 

Linear Hypotheses:
           Estimate lwr      upr     
B - A == 0   8.3520  -1.5619  18.2659
C - A == 0   4.7300  -5.1839  14.6439
D - A == 0  16.8550   6.9411  26.7689
C - B == 0  -3.6220 -13.5359   6.2919
D - B == 0   8.5030  -1.4109  18.4169
D - C == 0  12.1250   2.2111  22.0389