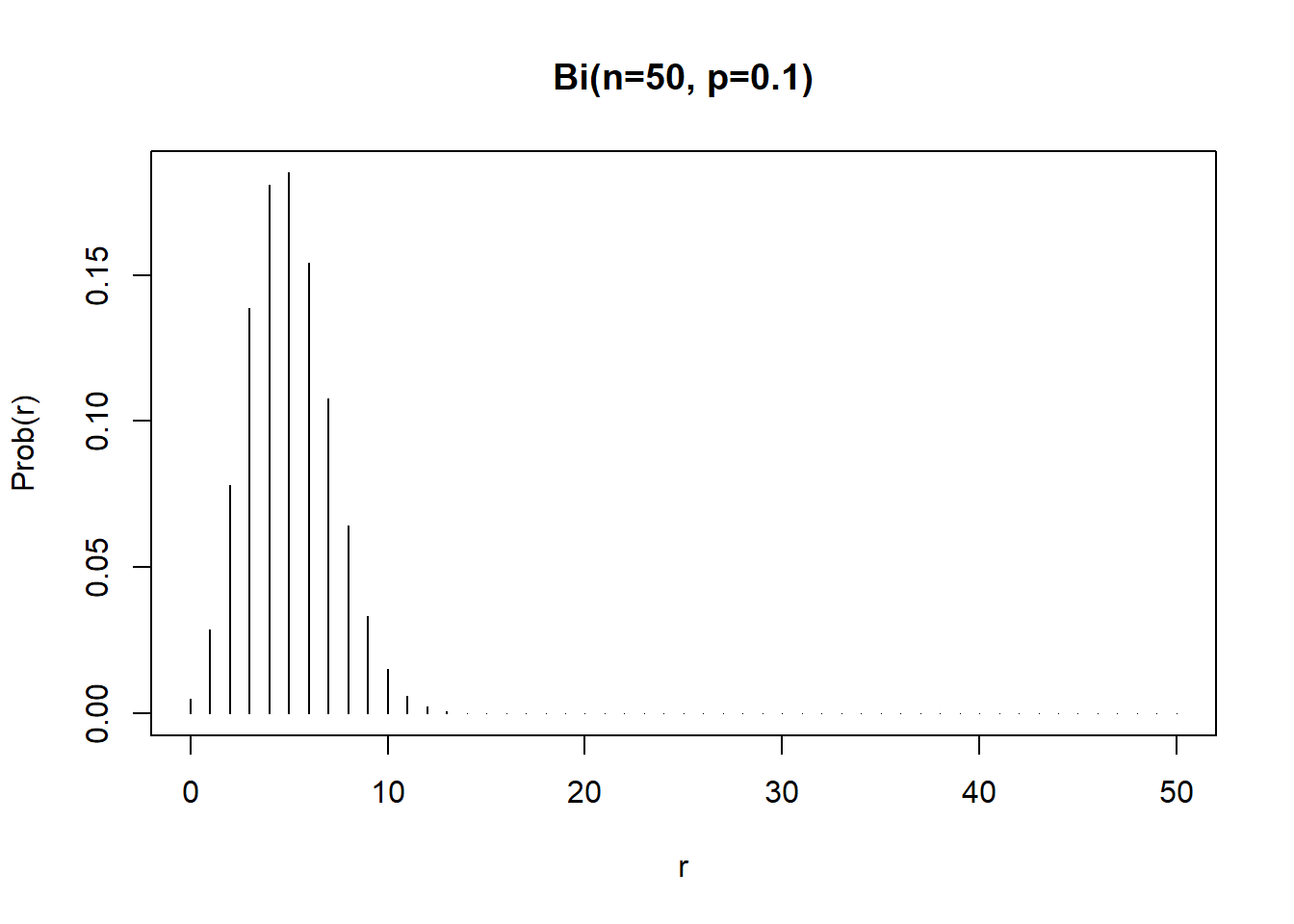Section 49 Binomial Distribution: Example
49.1 Example 1
If \(X\) denotes the number of heads from 10 tosses of a coin, where the probability of heads in any one toss is 0.7, then we write: \(X \sim Bin(10,0.7)\)
Find the probabilities for the Binomial distribution.
What is the probability of 3 or fewer successes i.e. \(Pr(X<=3)\)?
What is the probability of 4 or more successes i.e. \(Pr(X>=4)\)?
49.2 Example 2
Here are some further examples of binomial distributions.
binom_prob <- dbinom(0:20,size=20,prob=0.2)
plot(0:20, binom_prob, type="h",
main="Bi(n=20, p=0.2)",
xlab="r", ylab="Prob(r)")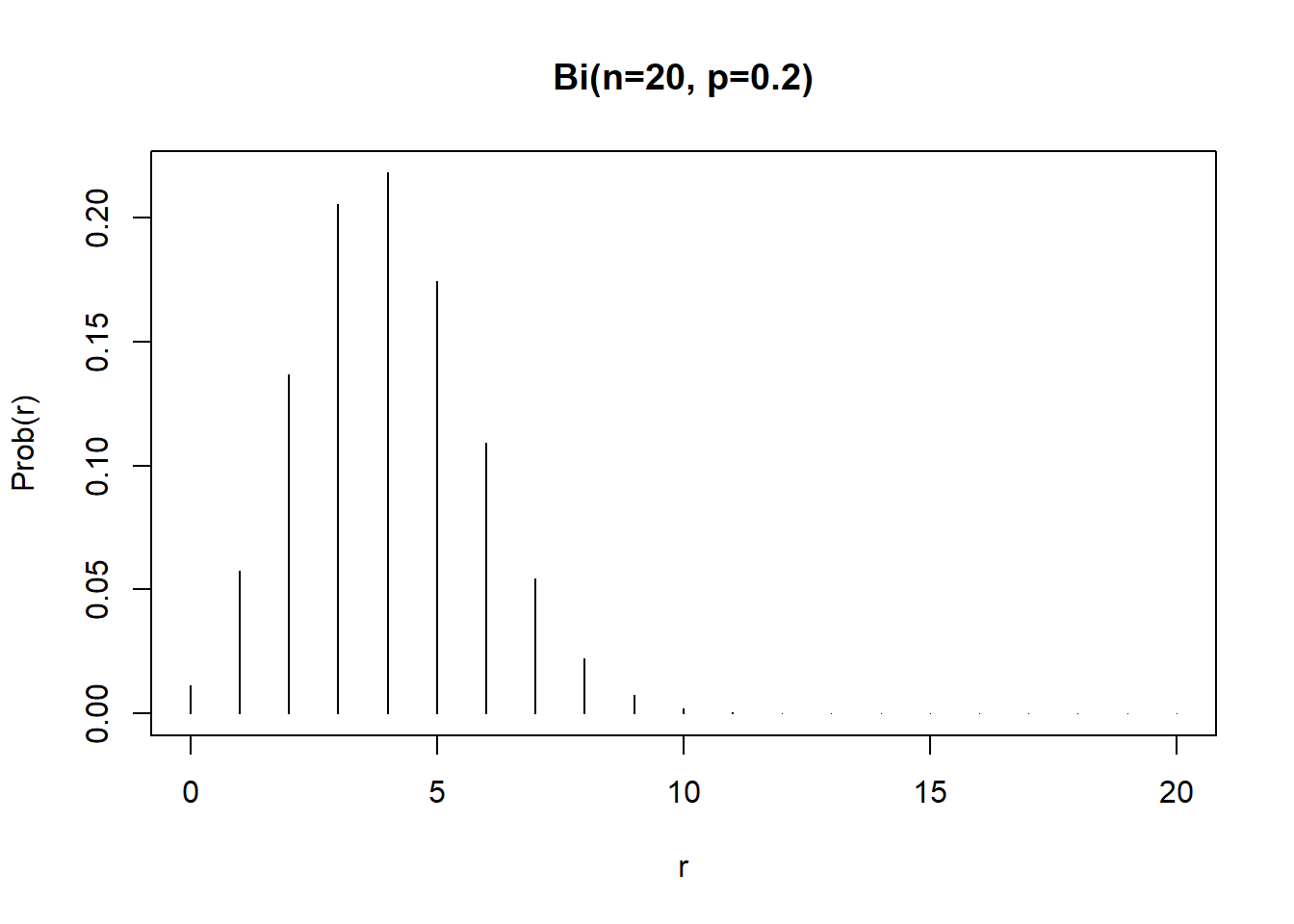
binom_prob <- dbinom(0:20,size=20,prob=0.5)
plot(0:20, binom_prob, type="h",
main="Bi(n=20, p=0.5)",
xlab="r", ylab="Prob(r)")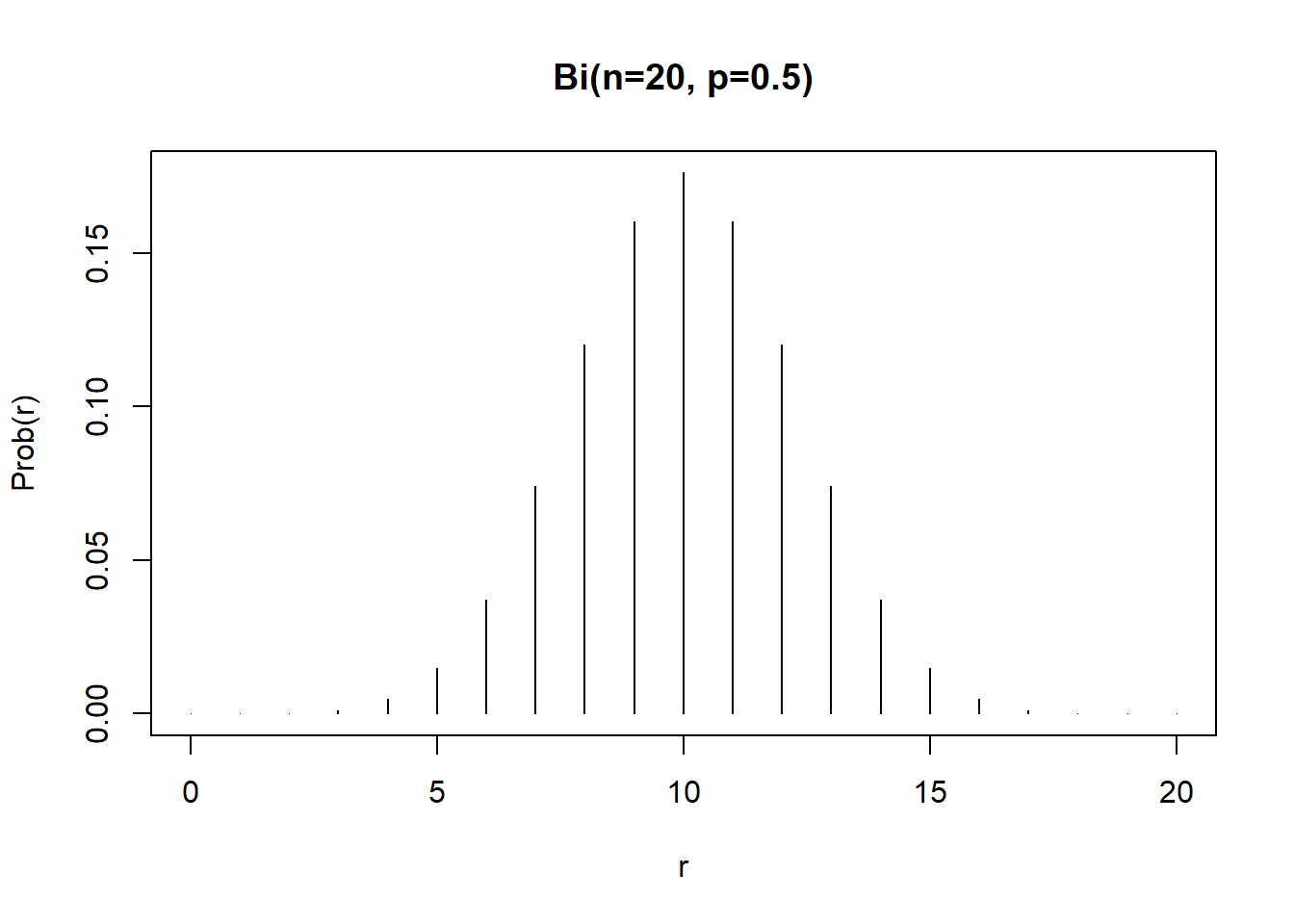
binom_prob <- dbinom(0:50,size=50,prob=0.1)
plot(0:50, binom_prob, type="h",
main="Bi(n=50, p=0.1)",
xlab="r", ylab="Prob(r)")