Section 26 Correlation

Correlation

• It is a measure of association between continuous variables

• Karl Pearson developed the correlation coefficient from a similar but slightly different idea by Francis Galton

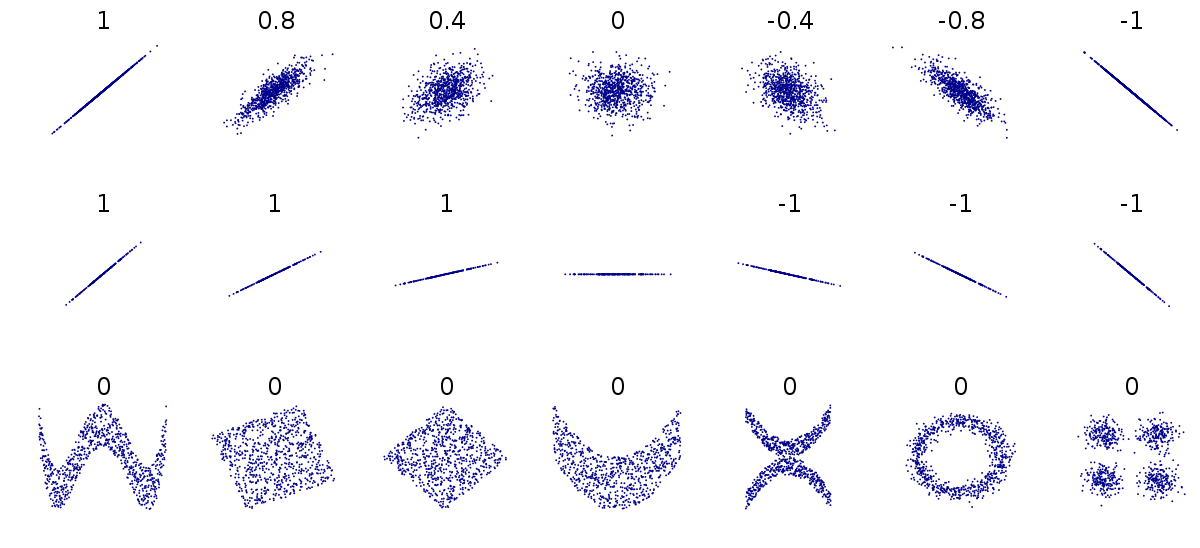
• It only applies to the linear relationship

• The estimate of correlation lies between -1 and +1 - Values less than zero imply negative correlation - Values greater than zero imply positive correlation - Values close to 1 or -1 imply strong correlation - Values close to 0 imply little or no correlation

• Correlation does NOT imply causation

• Rank correlation coefficients, such as Spearman’s rank correlation coefficient and Kendall’s rank correlation coefficient, measure the association of two variables without a linear relationship condition.

• Note that correlations are symmetric in the sense that r(x,y) = r(y,x).

• Formula of correlation: Uses covariance and variance of two variables x & y

• Centering and Scaling of the data x & y

Formula of Correlation Coefficient

$$\large r_{xy} = \frac{Cov(x,y)}{\sqrt{(Var(x)Var(y)}} = \frac{Cov(x,y)}{s_xs_y}$$

$$\large Cov(x,y) = s_{xy} = \frac{1}{n-1}\sum\limits_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})$$

$$\large Var(x) = s_x^2 = \frac{1}{n-1}\sum\limits_{i=1}^{n} (x_i-\bar{x})^2$$

$$\large Var(y) = s_y^2 = \frac{1}{n-1}\sum\limits_{i=1}^{n} (y_i-\bar{y})^2$$