Section 52 Poisson Distribution: Example

52.1 Example 1

If at a certain time of the day the number of cars queuing at a specific set of traffic lights is well described by a Poisson distribution with mean 3.1, then we write: \(X \sim Po(\lambda=3.1)\)

The probability that the queue has 9 or fewer cars will be : ppois(q=9, lambda=3.1)

Therefore the probability the queue has more than 9 cars is 1 - 0.9986 or 0.0014.

To find all the Poisson probabilities and the shape of the probability function is dpois

    pois_prob = dpois(0:20,lambda=3.1)
    plot(x=0:20, pois_prob, type="h", 
         main="Po(3.1)", 
         xlab="r", ylab="Prob(r)")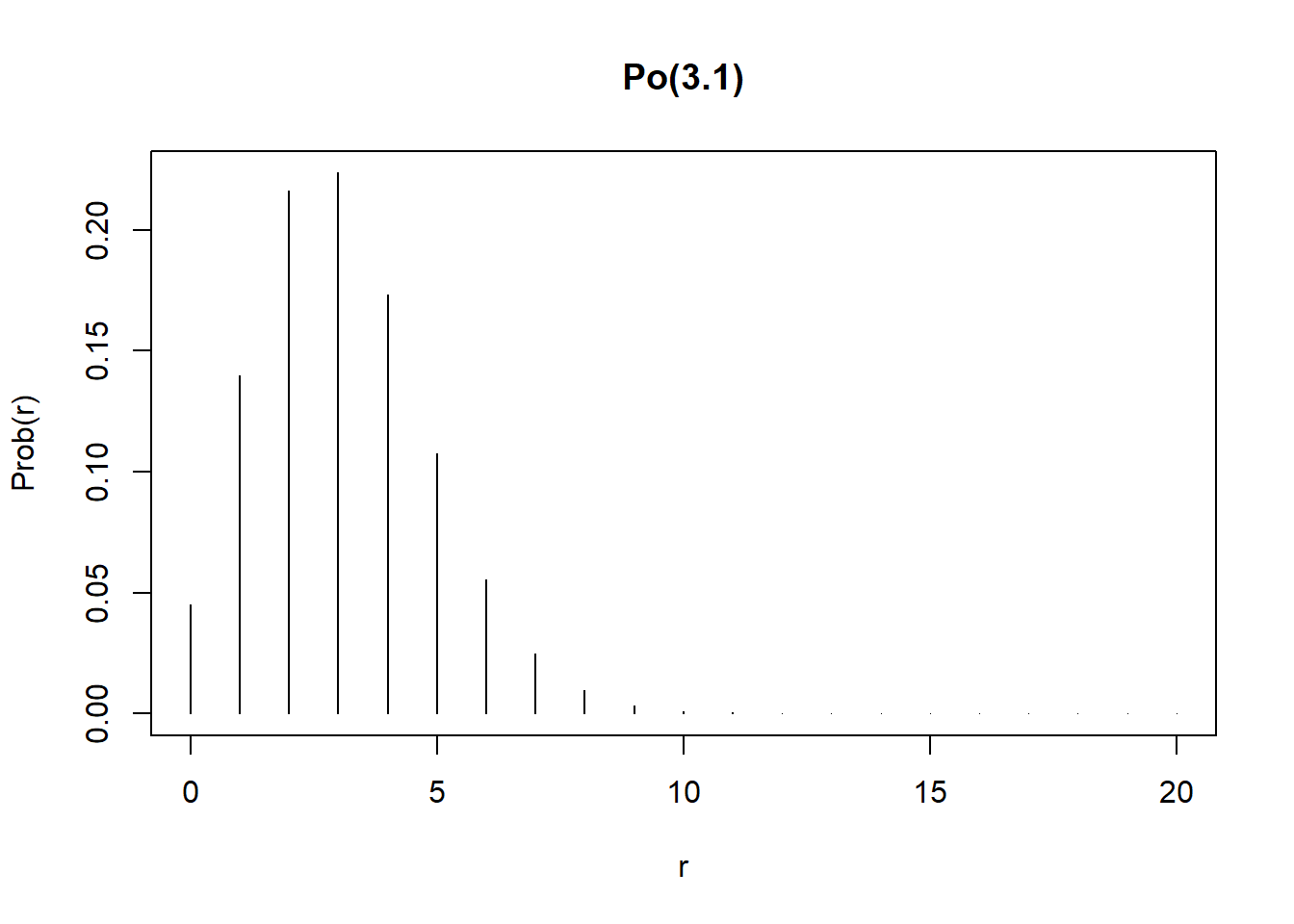

52.2 Example 2

• Generate 50 values from a Poisson distribution with mean=4.0, plot them and describe the shape of their distribution.

• Is it symmetric?

• What are the sample mean and standard deviation? What should they be?

• An interesting and important feature of the Poisson distribution is that its variance is the same as its mean.

52.3 Example 3

• Assume that the number of beetles found on a plant follows a Poisson distribution with mean 5.

• Derive a sample of 100 observations from such plants and plot the data.

• What are the mean, variance and sd of these counts?

• How many plants would you expect to have more than 5 beetles?

• How many would you expect not to have any beetles?